Probably the greatest advantage of studying the DP over the more general random manifold models is the ease of carrying out numerical simulations. These may be done both in the original framework or as surface growth simulations, which are related by the mapping of the previous section. I will concentrate here on the former, which gives us direct access to the physically relevant quantities. Numerical methods have been extremely important in establishing the properties of DP models.
A particularly appealing numerical method for understanding the equilibrium properties of DP models is the transfer matrix algorithm[10]. This is formulated on lattice models of the DP. Generally, the DP is taken as an oriented path on the links of a lattice. For each step along the x direction, the path is allowed to step forward, to the left, or to the right, with an increased energy cost for motion to the left or right, which models the elasticity of the DP. An even simpler model is possible, in which the path is oriented along the diagonal of an N+1-dimensional (hyper)-cubic lattice, and is allowed to step along any of the 2N oriented links available to it. In this case, there is no explicit elasticity to the DP, but the motion is restricted in the transverse direction, and it is believed that this constraint is sufficient to maintain the DP universality class. A random potential is included as a random uncorrelated energy on either the bonds or the links of the lattice.
The transfer matrix method proceeds essentially by using the group property of the partition function,
![]()
where we have gone to a discrete-time formulation appropriate for the
lattice. This is just a restatement of the physically obvious fact
that all paths of a DP ending at point ![]() at position x+1
must pass through some other point
at position x+1
must pass through some other point ![]() at position x. The
transfer matrix algorithm has the additional advantage that it may be
formulated directly at zero temperature, to find the energy of the
optimal path ending at a particular point
at position x. The
transfer matrix algorithm has the additional advantage that it may be
formulated directly at zero temperature, to find the energy of the
optimal path ending at a particular point ![]() . In this case
the recursion relation becomes
. In this case
the recursion relation becomes
![]()
Because the transfer matrix algorithm can be simply iterated, the
computational time simply scales linearly with the size of the matrix
and with the length of the DP. Typically, one calculates quantities
in a finite box of with W for a DP of length L. This gives a time
![]() . Roughly speaking, one should scale W with the
roughness of the DP to avoid severe boundary effects to get
. Roughly speaking, one should scale W with the
roughness of the DP to avoid severe boundary effects to get ![]() . While this exponent can be fairly large for large N,
it is still a polynomial time algorithm which exactly calculates
the energies for a particular realization of disorder. Using it, one
can obtain very accurate values for the exponents.
. While this exponent can be fairly large for large N,
it is still a polynomial time algorithm which exactly calculates
the energies for a particular realization of disorder. Using it, one
can obtain very accurate values for the exponents.
Furthermore, by a small modification of the method (with a concurrent extra computation cost), one can obtain the ground state configurations of the DP for particular realizations of randomness. A particularly beautiful example is given in Ref.[10], where a set of optimal paths for a DP anchored at the origin is shown as the position of the endpoint is varied. The resulting tree structure is quite striking. I have schematically indicated such a structure in Fig. 7\ (because I do not have a postscript copy of the original figure, I could not include it here).

Figure 7: ``Artist's'' conception of the optimal paths of a DP anchored
at both ends, as the position of one endpoint is varied. Note the
presence of widely separated configurations (``states'') separated by
very small energies, as indicated by the pair of thickly drawn paths.
It also has important implications for the structure of the low-energy
excitations and of the equilibrium behavior at finite temperature. To
see this, let's look at the behavior of the paths as we change the
end-point position. Imagine we allow the DP to
find a global optimal path, which ends at some particular ![]() .
If we then move the endpoint slightly, there is a very high
probability that the optimal path with be essentially unchanged,
adjusting only near the end-point. As we continue to move the
endpoint, eventually we jump to a new, larger scale branch of the
tree. Then the optimal DP stays on that branch for some short
distances, and again we jump. Moving further and further, we
eventually see larger and larger (but also rarer and rarer) jumps of
the optimal path. At the points at which the path makes a large jump,
the energy difference between the two paths must be very small -
otherwise the path would not make a large jump, but simply adjust one
or the other path.
.
If we then move the endpoint slightly, there is a very high
probability that the optimal path with be essentially unchanged,
adjusting only near the end-point. As we continue to move the
endpoint, eventually we jump to a new, larger scale branch of the
tree. Then the optimal DP stays on that branch for some short
distances, and again we jump. Moving further and further, we
eventually see larger and larger (but also rarer and rarer) jumps of
the optimal path. At the points at which the path makes a large jump,
the energy difference between the two paths must be very small -
otherwise the path would not make a large jump, but simply adjust one
or the other path.
The tree structure thus implies the existence of rare widely separated
pairs of states very close in energy. We expect this to be the case
for the ground state as well, so this implies the existence of rare
large, anomalously low-energy excitations of the DP. They are
anomalous because typical excitations of size L have energies
of order ![]() .
.
Even at low temperatures in equilibrium, these rare large low-energy excitations will be present due to thermal activation! We can make this prediction quantitative by considering the distribution of energies of excitations of size L. From scaling, we expect
![]()
It is natural to assume a smooth form for f, such that ![]() . Then, at low temperatures, the probability of finding an
excitation of energy less than T of size L is
. Then, at low temperatures, the probability of finding an
excitation of energy less than T of size L is
![]()
Now consider the fluctuations of the DP around its ground state at finite temperature. This is
![]()
where the brackets denote a thermal average. The contribution of the
large, rare excitions to the ![]() moment of this is
moment of this is
![]()
These fluctuations are in fact anomalously large (they grow with L,
despite our belief that the ground state is stable!). They dominate
at large L over the contributions from the smaller scales, and in
particular from the typical fluctuations of order ![]() . Note that, for n=2, the identity
. Note that, for n=2, the identity ![]() implies that
implies that
![]()
The variance of the thermal fluctuations actually scales just as it
does in the absence of disorder (i.e. like a random walk). In fact,
this result can be shown exactly (with a coefficient ![]() )
for any random manifold model.
)
for any random manifold model.
EXERCISE: Derive the generalization of the scaling of the moments of the thermal fluctuations for manifolds of general dimension.
In fact, an additional exact result in known for the case N=1. This is due to a special fluctuation-dissipation result, first obtained by Forster, Nelson and Stephen. We start from the KPZ equation, Eq. 127 and assume a white-noise random potential
![]()
One may derive a Fokker-Planck equation for the
probability distribution ![]() . Such Fokker-Planck
equations generally are insoluble, but in this special case an exact
stationary ``equilibrium-like'' solution can be found,
. Such Fokker-Planck
equations generally are insoluble, but in this special case an exact
stationary ``equilibrium-like'' solution can be found,
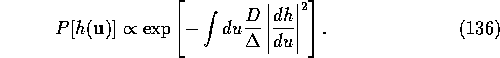
Using this result, one may directly calculate the equal x correlations,
![]()
Since this is an energy fluctuation, we expect
![]()
since ![]() . This implies
. This implies ![]() , which,
along with
, which,
along with ![]() implies
implies
![]()